Расчетные моменты инерции и сопротивления
для геометрических форм конструкций

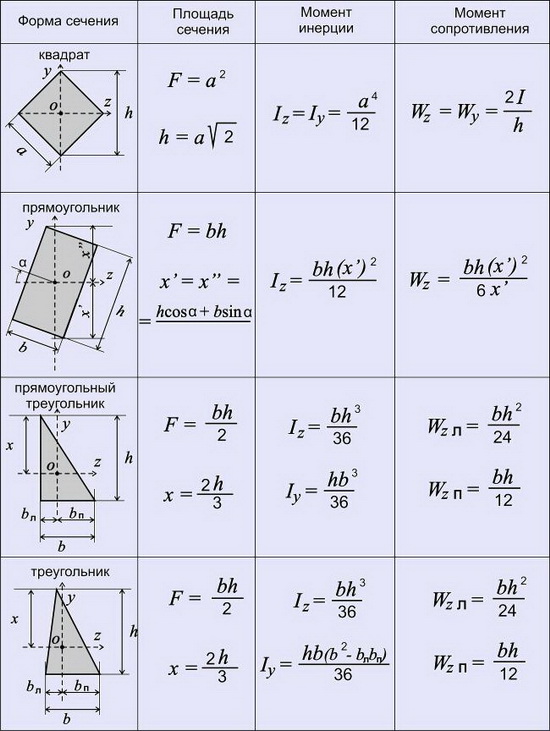
Приведены наиболее часто употребляемые формы сечений строительных конструкций.

Обычно, этих формул достаточно для большинства расчетов, но случаи бывают всякие и сечение конструкции может быть не такой простой геометрической формы или положение осей, относительно которых нужно определить момент инерции или момент сопротивления, может быть не таким, тогда можно воспользоваться следующими формулами:

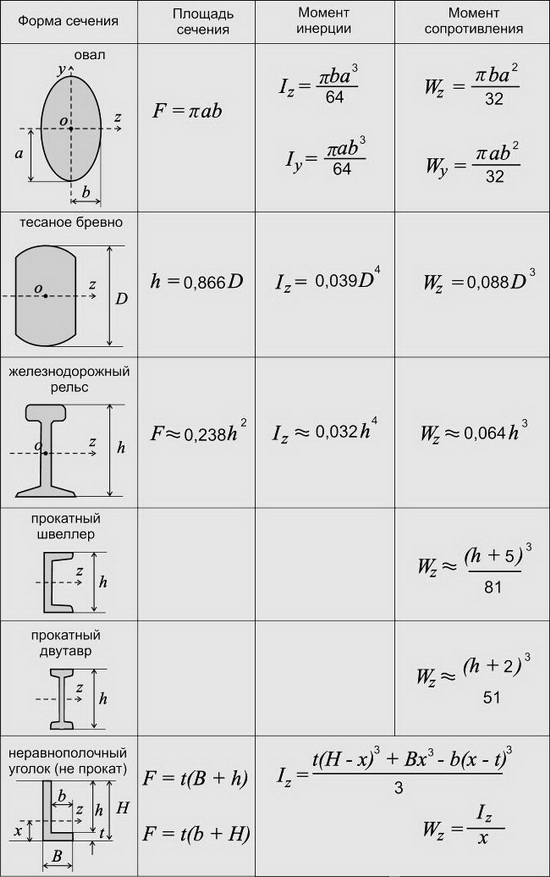
Как видно из таблицы, высчитывать момент инерции и момент сопротивления для неравнополочных уголков достаточно сложно. Поэтому для неравнополочных и равнополочных прокатных уголков, а также для швеллеров, двутавров и профильных труб есть сортаменты. В сортаментах значения момента инерции и момента сопротивления приводятся для каждого профиля.

Если же у вас сложносоставное сечение, можете воспользоваться следующими рекомендациями.

W - это момент сопротивления поперечного сечения балки, другими словами, площадь сжимаемой или растягиваемой части сечения балки, умноженная на плечо действия равнодействующей силы. Момент сопротивления необходимо знать для расчетов конструкции на прочность, т.е. по предельным напряжениям и для определения углов поворота поперечного сечения и прогиба (смещения) центра тяжести поперечного сечения, так как максимальные деформации возникают в самом верхнем и в самом нижнем слое изгибаемой конструкции, то определить момент инерции можно, умножив момент сопротивления на расстояние от центра тяжести сечения до верхнего или нижнего слоя. Поэтому для прямоугольных сечений I = W·h/2.

При определении момента инерции сечений сложных геометрических форм сначала сложная фигура разбивается на простейшие, затем определяются площади сечения этих фигур и моменты инерции простейших фигур, затем площади простейших фигур умножаются на квадрат расстояния от общего центра тяжести сечения до центра тяжести простейшей фигуры. Момент инерции простейшей фигуры в составе сложного сечения равен моменту инерции фигуры + квадрат расстояния умноженный на площадь. Затем полученные моменты инерции суммируются и получается момент инерции сложного сечения. Но это максимально упрощенные формулировки.