Представлены расчетные схемы, различные виды действующих нагрузок, эпюры сил, отображающие характер изменения касательных напряжений, эпюры изгибающих моментов, отображающие характер изменения нормальных напряжений, возникающих в поперечном сечении балки, а также формулы для определения опорных реакций, действующего изгибающего момента, максимального изгибающего момента, формулы для определения прогиба балки на расстоянии х от начала балки и формулы для определения максимального прогиба балки, а также формулы для определения тангенса угла поворота поперечного сечения на опорах и на концах - для консольных балок. Классификация производилась не по действующим нагрузкам, а по виду опор балки. В данном разделе представлены статически определимые балки.
Ось х, относительно которой производятся расчеты изгибающего момента и прогиба, соответствует продольной оси, проходящей через центр тяжести поперечных сечений балки. Значение момента инерции I следует определять относительно оси z .
Если в таблицах отсутствует формула для определения прогиба на каком-то из участков балки (из-за чрезмерной длины формулы), то опять же ее можно вывести, дважды должным образом проинтегрировав уравнение изгибающего момента, разделив результат на EI и добавив к этому результат интегрирования угла поворота.
В общем виде уравнение для определения углов поворота выглядит так:
θх = - θA + Мх/EI + Ax2/2EI - qx3/6ЕI
например, для шарнирной балки, к которой приложена сосредоточенная нагрузка (таблица 1, №1.1, момент и распределенная нагрузка осутствуют) на участке от начала балки до точки приложения силы (0 < x < l/2) уравнение будет иметь вид:
θх = - θA + Ax2/2EI = - Ql2/16EI + Qx2/4EI = Q(4x2 - l2)/16EI
Соответственно в общем виде уравнение для определения прогиба выглядит так:
fх = - θAx + Мх2/2EI + Ax3/6EI - qx4/24ЕI
для той же шарнирной балки на участке от начала балки до точки приложения силы (0 < x < l/2) уравнение будет иметь вид:
fх= - θAx + Ax3/6EI = - Ql2x/16EI + Qx3/12EI = Qx(4x2 - 3l2)/48EI
На участке от точки приложения силы до конца балки (l/2 < x < l) уравнение будет иметь вид:
fх = - θAx + Ax3/6EI - Q(x - l/2)3/6EI
Эпюры углов поворота и прогибов поперечного сечения по длине балки не приводятся. Если в формуле прогиба есть знак минус, то это значит, что балка прогибается вниз (что в общем-то логично), а если быть более точным, то центр тяжести поперечного сечения смещается вниз по оси у.
Представленные расчетные схемы позволяют рассчитать балку практически при любом возможном виде нагрузки. Если на балку действует несколько различных нагрузок, то можно производить отдельный расчет для каждой схемы загружения, а затем полученные результаты сложить (с учетом знаков). Это правило называется принципом суперпозиции и в некоторых случаях значительно упрощает общий расчет, а также экономит уйму времени на поиск в сети подходящей расчетной схемы.
1. БАЛКА НА ДВУХ ШАРНИРНЫХ ОПОРАХ
 2. КОНСОЛЬНАЯ БАЛКА
2. КОНСОЛЬНАЯ БАЛКА
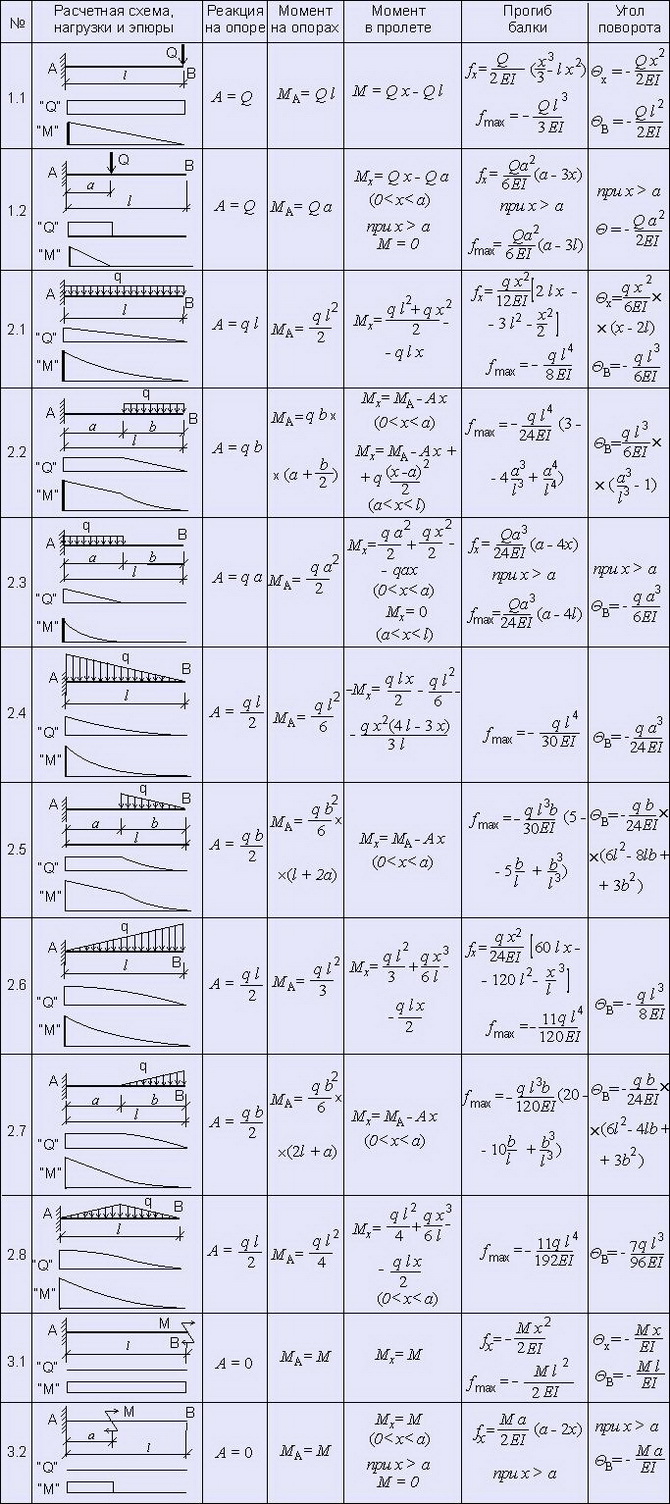 3. БАЛКА НА ШАРНИРНЫХ ОПОРАХ С КОНСОЛЯМИ
3. БАЛКА НА ШАРНИРНЫХ ОПОРАХ С КОНСОЛЯМИ
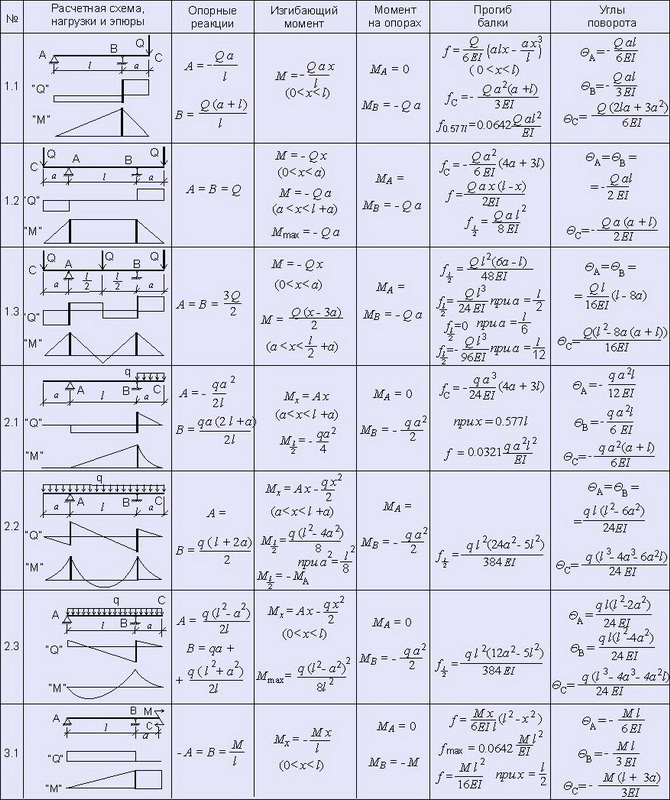
Расчетные схемы для статически неопределимых балок смотри здесь.
| 
