Поликарбонат - достаточно новый строительный материал. В том смысле, что в Советском Союзе поликарбонат не использовался, а потому не было никаких ГОСТов или СП, регламентирующих параметры и свойства поликарбоната. Не появились подобные нормативные документы и за последние 20 лет использования поликарбоната. В основном потому, что производится поликарбонат все больше за границей или на совместных предприятиях и отвечает требованиям пока мало известных нам норм.
Зато рекламных материалов, посвященных удивительным и невероятным свойствам поликарбоната, в сети немало. И про прекрасные прочностные свойства, типа в 200 раз прочнее стекла, и про чудесные упругопластические свойства, мол, выгибать можно по достаточно малому радиусу, и светопроницаемость лучше, чем у стекла и срок службы огромный, чуть ли не 20 лет, и так далее. Все это, конечно, очень хорошо, но для расчета конструкций нужны несколько другие данные, а именно геометрические характеристики поперечного сечения, расчетное сопротивление сжатию и растяжению (если разное), модуль упругости. А такой информацией ни производители, ни продавцы делиться не торопятся, потому как вместе с поликарбонатом к нам с Запада пришла узкая специализация.
Конечно же имеется большое количество пособий по расчету и монтажу поликарбоната, в которых приводятся достаточно подробные описания монтажа и сводные таблицы для определения шага обрешетки и минимального радиуса гиба, но при этом часто добавляется, что для получения более точных данных необходимо произвести инженерный расчет. И все это очень удобно, да только пособия эти как будто все писаны под копирку, а между тем оборудование, добавки и прочие тонкости технологии у разных производителей разные и то, что рекомендации подходят одинаково хорошо для поликарбоната, выпущенного различными компаниями - не факт.
Мы тоже не сможем внести большую ясность в вопрос расчета конструкций с использованием поликарбоната, а только попробуем, основываясь на разрозненных данных различных руководств и рекомендаций. Наиболее полной и внятной представляется информация о поликарбонате компании Polygal, прошедшем не просто сертификацию в России, но и испытание образцов в ГУП «ЦНИИСК им. Кучеренко» (Сертификат Госстроя № 00018368).
Примечание: Как правило вся продукция, реализующаяся на отечественном рынке, проходит сертификацию и соответствует неким техусловиям, однако методика тестирования DIN53457 или DIN53455 нашему человеку мало о чем говорит, а вот данные, полученные при испытании образцов по ГОСТам, заслуживают больше доверия, к тому же данные, полученные при испытании образцов по ГОСТам, несколько отличаются от данных, полученных при испытании образцов по методике DIN - немецкого института по стандартизации.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ РАСЧЕТОВ
В настоящее время в строительстве используется листовой (монолитный) поликарбонат и сотовый (ячеистый) поликарбонат. Прочностные и упругие характеристики листового и сотового поликарбоната зависят не только от характеристик исходного материала, но и от особенностей производства. Например, для вышеуказанного сотового поликарбоната Polygal прочность при растяжении Rр для плит высотой (толщиной) 8 мм составляет 653 кгс/см², для плит высотой 10 мм - 658 кгс/см², для плит высотой 16 мм (трехполочных) - 705 кг/см². Соответственно модуль упругости для плит высотой 8 мм составляет 20400 кгс/см², для плит высотой 10 мм - 21300 кгс/см², для плит высотой 16 мм (трехполочных) - 22770 кг/с². Испытания образцов плит сотового поликарбоната высотой 4 и 6 мм не проводились, однако анализ приведенного ряда позволяет предположить, что прочность на растяжение для таких плит будет также в пределах 630-640 кгс/см², а модуль упругости - в пределах 20000 кгс/см².
Однако любой человек, хотя бы немного знакомый с основами сопромата, знает, что при работе конструкции могут возникать не только растягивающие, но и сжимающие напряжения. Например при использовании поликарбоната в качестве прозрачного настила кровли поликарбонат следует рассматривать как балку, в одной части поперечного сечения которой возникают растягивающие напряжения, а в другой - сжимающие, т.е. конструкция работает на изгиб. Тем не менее, для многих материалов сопротивление сжатию значительно больше, чем сопротивление растяжению. Поликарбонат в этом - не исключение, так приводимая для поликарбоната других компаний максимальная прочность на изгиб составляет 900-950 кгс/см², хотя для монолитного поликарбоната можно встретить и значение 250-300 кгс/см². Все это усложняет и без того не простой процесс расчета поликарбоната, но чтобы максимально упростить расчеты предлагается использовать следующие данные:
| Наименование показателя |
Величина |
| Предел прочности при растяжении Rp, МПа |
60-70 |
| Модуль упругости при растяжении Ep, МПа |
2000 - 2600 |
| Удлинение при растяжении, % |
5 - 7 |
| Удлинение при разрыве, % |
80 - 100 |
| Предел прочности при изгибе Rи, МПа |
90 - 110 |
| Модуль упругости при изгибе Eи, МПа |
2200 - 2500 |
| Предел прочности при сжатии Rс, МПа |
80-100 |
| Модуль упругости при сжатии Eс, МПа |
2300 - 2500 |
| Плотность, г/cм³ |
1,2 |
Геометрия поперечных сечений сотового поликарбоната может достаточно сильно различаться в зависимости от производителя. Но и здесь за основу можно принять параметры листов Polygal:
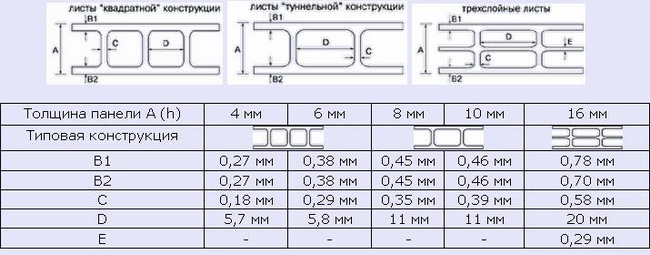
рис.1
Для листового, так называемого монолитного поликарбоната геометрические характеристики - это размеры листа 2,05х3,05 м при толщине листа 2, 3, 4, 5, 6, 8, 10 и 12 мм. Толщина сотового поликарбоната, кроме указанных, также может быть еще 20, 25 и 32 мм.
В принципе этих данных достаточно для расчета большинства конструкций в который используется листовой или сотовый поликарбонат, имеющий сходные характеристики.
ПРИМЕР РАСЧЕТА ПЛОСКОГО НАСТИЛА
ИЗ МОНОЛИТНОГО ПОЛИКАРБОНАТА
Основной нагрузкой для плоского настила из поликарбоната будет снег и ветер. При этом снеговая нагрузка как правило действует сверху, а ветровая - как сверху так и снизу. Как правило ветровая нагрузка в несколько раз меньше снеговой, а для отдельно стоящих конструкций, когда нет стены или другого препятствия, меняющего направление ветра, ветровая нагрузка уменьшается еще в несколько раз. Таким образом снеговая нагрузка может привести к чрезмерному прогибу листов настила, а ветровая нагрузка к срыву листов. Конечно же существуют и другие атмосферные осадки, например, дождь и град, однако нагрузки от этих осадков для поликарбоната не являются критическими (если град не аномальных размеров). К тому же ветровая нагрузка сверху будет приводить к уменьшению снежного покрова, а значит и к уменьшению снеговой нагрузки, поэтому для расчета прочности плоского настила достаточно использовать только снеговую нагрузку и даже собственный вес листа можно не учитывать ввиду очень малого значения этого показателя. Расчет крепления поликарбоната на действие ветровой нагрузки приводится отдельно.
Снеговая нагрузка зависит от местности. Для Москвы расчетную нагрузку можно принимать равномерно распределенной и равной 180 кг/м², а для листа шириной 1 м q = 180 кг/м или 1,8 кг/см.
Момент сопротивления монолитного листа поликарбоната высотой (толщиной) h = 2 мм (0,2 см) при расчетной ширине b = 1 м (100 см) составит:
Wz = bh² / 6 = 100·0,2² / 6 = 0,667 см³
Тогда максимальный изгибающий момент составит
М = WzRи = 0,667·610 = 406,67 кг·см
Это означает, что если монолитный поликарбонат будет иметь только две опоры, то максимальное расстояние между опорами составит
l = √(8M/q) = √(8·406,67/1,8) = 42,51 см
Если пролетов между балками обрешетки будет 2 и более и длина пролетов будет одинаковой, то (приблизительно)
l = √(12M/q) = √(12·406,67/1,8) = 52,1 см
Поликарбонат - достаточно пластичный материал. При двух опорах максимальный прогиб листа составит
f = 5ql4/384EI =5·1.8·42,514/384·22500·0,667·0,1 = 51,04 см
Примечание: Момент инерции Iz = bh3/12 = Wzh/2.
В реальности такого большого прогиба быть конечно же не может. Просто потому, что для такого прогиба потребуется или уменьшение расстояния между опорами листа более чем в 2 раза при сохранении длины листа, или запас листа на опорах, позволяющий длине листа увеличиться более чем в 2 раза. Тем не менее этот расчет является очень показательным, в том смысле, что позволяет приблизительно определить минимальный радиус изгибания листа (об этом чуть позже). При наличии 3 и более опор при тех же пролетах 42,5 см максимальный прогиб будет в крайних пролетах и будет приблизительно в 2,5 раза меньше, но легче от этого не станет, максимально допустимый прогиб, рекомендуемый производителями должен составлять не более 1/20 пролета, в данном случае не более 2,1 см. Но заказчику и такой прогиб на 42,5 см может показаться достаточно большим, отсюда вывод:
при расчете поликарбоната главным является расчет по деформациям
Например, для монолитного листа толщиной 8 мм (т.е. толщина листа в 4 раза больше по сравнению с 2 мм) момент инерции увеличится в 43 = 64 раза (Iz = 0,06667·64 = 4,2667 см4) и прогиб такого листа при том же пролете и при той же схеме закрепления будет уже 0,797 см. А если сделать для такого листа опирание по периметру, то прогиб еще уменьшится, если контур будет представлять собой квадрат, то прогиб уменьшится приблизительно в 2 раза.
Все в приведенном расчете вроде бы хорошо, да только не учтена экономическая составляющая. Дело в том что сотовый поликарбонат стоит дешевле монолитного, да и весит при той же толщине меньше, а потому использовать его более соблазнительно, к тому же эффективность использования материала у сотового поликарбоната в несколько раз больше. А потому пришло время рассмотреть
ПРИМЕР РАСЧЕТА ПЛОСКОГО НАСТИЛА
ИЗ СОТОВОГО ПОЛИКАРБОНАТА
Чтобы определить момент инерции поперечного сечения сотового поликарбоната нужны точные геометрические характеристики сечения. Представленные выше данные не являются совсем точными, так как визуально видно, что переход из полок в стенку плавный, т.е. имеется некий радиус перехода, значение которого остается неизвестным. Для упрощения решения задачи можно не обращать на этот самый радиус внимания, а рассматривать поперечное сечение сотового поликарбоната, как двутавровую балку (точнее несколько двутавровых минибалок) у которой есть нижняя и верхняя полка с указанной толщиной и стенка с указанной толщиной. Это значительно упростит расчеты и даст относительно небольшой запас по прочности.
Тогда ширина одной балки составит b = D + C = 1,1 +0,035 = 1,135 см, а момент инерции для поперечного сечения сотового поликарбоната высотой 8 мм составит:
Iz = Σ(Iz + y²F) = 2·1,135·0,0453/12 + 2·1,135·0,045(0,4 - 0,045/2)² + 0,035(0,8 - 0,045·2)3/12 = 0,000017237 + 0,014557 + 0,001044 = 0,01561 см4
В одном метре помещается 100/1,135 = 88,1 такая балка, значит, момент инерции для листа шириной 1 м составит:
Iz = 0,01561·88,1 = 1,376 см4
При двух опорах и при том же пролете (чтобы расчет был более показательным) прогиб листа составит
f = 5ql4/384EI =5·1,8·42,514/384·22500·1,376 = 2,47 см
При 4 и более опорах и при том же расстоянии между опорами (чтобы расчет был более показательным) максимальных прогиб листа будет в крайних пролетах и составит
f = ql4/185EI =1,8·42,514/185·22500·1,376 = 0,998 см
Примечание: Как видим, по сравнению с монолитным поликарбонатом прогиб при той же толщине листа 8 мм увеличится в 2,47/0,797 = 3,1 раза, при этом разница в расходе материала, а значит и в цене - более значительная (монолитный поликарбонат толщиной 8 мм обойдется около 60$ за м², а сотовый - около 8-10$ за м²).
Данная методика расчета позволяет подобрать по максимально допустимым деформациям поликарбонат нужной толщины, когда известны максимальная нагрузка и расчетная схема и наоборот, можно подобрать под планируемый поликарбонат расстояния между балками обрешетки. Сделать подобный расчет по широко предлагаемым сводным таблицам достаточно проблемно даже методом интерполяции (во всяком случае линейная интерполяция здесь не подходит). Кроме того, максимально допустимый прогиб, заявленный производителем, может быть значительно больше прогиба, ожидаемого заказчиком. А еще, в таблицах всегда учитывается опирание по четырем сторонам, а делается такое опирание не всегда, особенно если речь идет о небольших козырьках над входом.
С другой стороны, нельзя забывать и о том, что максимальный прогиб возможен только при максимальной снеговой нагрузке, которая бывает далеко не каждый год, а поликарбонат - не черепица, не то что на 200, даже на 20 лет никто гарантии не даст. Поэтому расчетную снеговую нагрузку можно и уменьшить на соответствующий коэффициент.
Важно:
Так как поликарбонат достаточно пластичный материал, то края листа желательно опирать на обрешетку не только по длине ската кровли (перпендикулярно рассматриваемым нами минибалкам, назовем эти опоры для краткости перпендикулярными), но и по ширине (параллельно минибалкам, на параллельные опоры). При этом снижается влияние местных нагрузок, а значит и деформаций на краях листа. А если листы будут стыковаться по ширине, то такое опирание позволит увеличить герметичность стыка и потому является скорее конструктивным требованием, чем расчетной необходимостью. Между тем в большинстве руководств по монтажу сотового поликарбоната рассматривается ситуация, когда сотовый лист поликарбоната имеет крайние и промежуточные параллельные опоры и только две крайние перпендикулярные опоры, при этом расстояние между перпендикулярными опорами может достигать и 6 и 12 метров, т.е. соответствовать длине листа.
Такая ситуация кажется несколько странной, так как в этом случае листы поликарбоната следует скорее рассматривать как балку переменного сечения в лучшем случае или как ферму с жестким закреплением в узлах в худшем случае (за исключением листов с Ж-образным сечением, довольно редких в наших местах). Расчет прочности и деформации балок переменного сечения - отдельная большая тема, ее здесь касаться не будем (итак наворочено уже достаточно), просто скажем - прогиб балки переменного сечения при таких геометрических характеристиках сечения будет намного больше, чем балки постоянного сечения. Для фермы с жестким закреплением стержней в узлах степень статической неопределимости будет исчисляться сотнями и для расчета такой фермы также потребуется достаточно мощный компьютер.
Тем не менее приблизительно определить несущую способность и прогиб сотового поликарбоната при опирании только на перпендикулярные опоры и только на параллельные опоры можно достаточно просто опытным путем. Для этого потребуется вырезать квадратный кусок из листа поликарбоната, чем большей будет величина стороны квадрата, точнее чем ближе она будет к величине проектируемого пролета, тем более показательным будет эксперимент. Далее достаточно взять два ровных бруска и расположить их параллельно так, чтобы расстояние между брусками в свету было на пару сантиметров меньше стороны квадрата. После этого квадратный лист укладывается на деревянные бруски, так чтобы минибалки были параллельны деревянным брускам, замеряется расстояние между основанием, на котором лежат бруски и низом листа, затем к листу прикладывается некоторая нагрузка и замеряется расстояние между основанием и низом листа при действующей нагрузке. Разница расстояний - это и есть прогиб листа под нагрузкой. Эксперимент повторяется, но уже при таком положении листа, когда минибалки расположены перпендикулярно деревянным брускам.
При написании статьи под рукой поликарбоната не было, а был только обрезок пластиковой панели толщиной 8 мм, с толщиной полок около 0,4-0,5 мм и расстоянием между стенками около 11,5 мм, т.е. геометрическими характеристиками похожий на рассматриваемый поликарбонат. Мы вырезали из панели квадрат со стороной около 24 см и провел несколько измерений. Разница прогибов даже при таком относительно небольшом пролете при параллельном и перпендикулярном опирании минибалок составила 8-10 раз. Не думается, что результаты для поликарбоната будут значительно отличаться, тем более что модуль упругости ПВХ сопоставим с модулем упругости поликарбоната. А потому
рассчитывать поликарбонатные листы только на параллельные опоры - не правильно.
Более корректными в этом отношении являются рекомендации по монтажу выше упоминавшихся панелей Polygal. Для таких плит большие расстояния между перпендикулярными опорами вообще не рассматриваются, а изменение расстояния между параллельными опорами приводит к незначительному изменению расстояния между перпендикулярными опорами. Например, при расчетной нагрузке 180 кг/м² для плит сотового поликарбоната толщиной 8 мм рекомендуемое расстояние между перпендикулярными опорами - 70 см, расстояние между параллельными опорами - 84 см. При расчете только на перпендикулярные опоры, т.е. по предложенному выше алгоритму прогиб в крайних пролетах составит
f = 0,998(70/42,51)4 = 2,71 см
что меньше 5% допустимого производителем прогиба 70/20 = 3,5 см.
Впрочем это имеет важность только для любителей плоских поверхностей, поликарбонат же хорош тем, что может значительно деформироваться, не теряя упругих свойств, другими словами, поликарбонат идеален для криволинейных конструкций. Чаще всего это арочные конструкции.
ПРИМЕР РАСЧЕТА АРОЧНОГО НАСТИЛА
ИЗ СОТОВОГО ПОЛИКАРБОНАТА
Когда мы рассчитывали прочность монолитного поликарбоната толщиной 2 мм, то определили, что прогиб - деформация - такого листа, благодаря хорошим упруго пластическим характеристикам может быть невероятно большим. Выгибание поликарбонатного листа - это также деформация материала, но как правило направленная в сторону, противоположную действующей нагрузке. Другими словами, когда из плоского листа выгибается арка, то таким образом создается предварительно напряженная конструкция. При этом на возможное изменение прочности можно не обращать внимания, так как основным все равно остается расчет по деформациям.
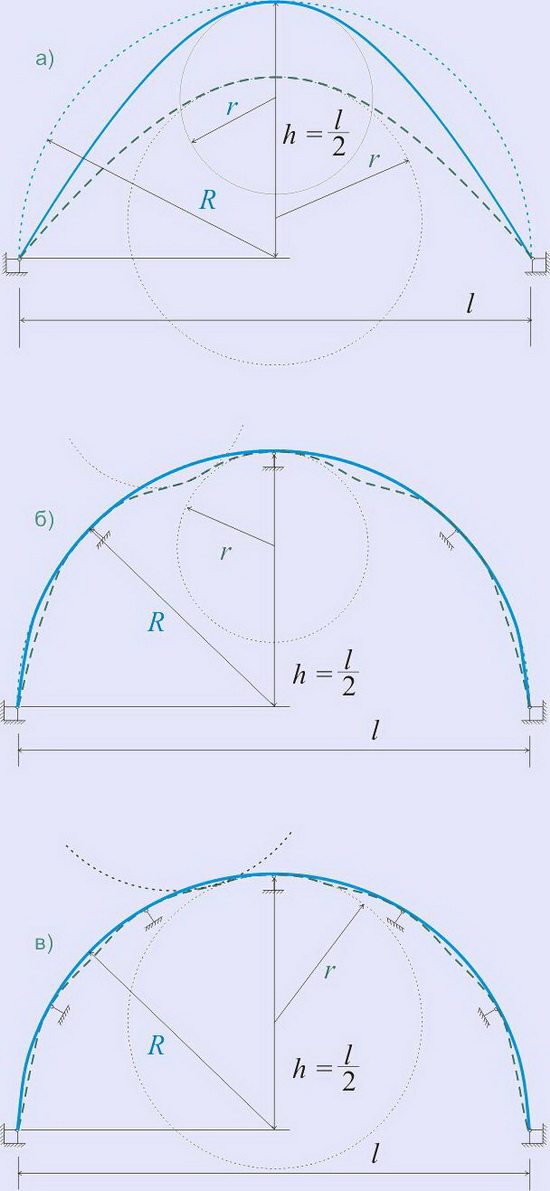
рис.2
Как видно из рисунка 2.а, выгнуть поликарбонат (как впрочем и лист из любого другого материала) так, чтобы центральная ось выгнутого листа описывалась уравнением окружности радиусом R - не получится. В результате распределения нормальных и касательных напряжений ось листа (значение прогиба) будет описываться параболой. Уравнение параболы не приводится, главное, понять суть. При этом в области максимальных напряжений ось поликарбонатного листа будет описываться окружностью радиусом r (голубого цвета). Этот радиус не может быть меньше минимально допустимого. Под действием нагрузки, например, равномерно распределенной, лист будет деформироваться, при этом ось листа примет вид, показанный на рисунке 2.а темно зеленым цветом. Это приведет к увеличению радиуса окружности, которая совпадает с осью в области максимальных напряжений. Радиус этой окружности обозначен также темно зеленым цветом. Если арочная конструкция будет представлять собой не половину окружности, как показано на рисунке 2, а например, 1/8 часть окружности (длина дуги между опорами на рисунке 2.б, а лучше 1/12 часть (длина дуги между опорами на рисунке 2.в, то изменение длины листа при деформации будет незначительным. В таких случаях запас прочности почти не уменьшится, так как увеличение радиуса изгиба увеличит значение нормальных напряжений - горизонтальных опорных реакций Nг (на рисунке не показаны), но одновременно снизит значение изгибающего момента, описываемого формулой Мх = Nгfх. Если длина арочной конструкции будет стремиться к длине половины окружности, как показано на рисунке, то значение нормальных напряжений будет увеличиваться с увеличением прогиба из-за увеличения значения горизонтальных опорных реакций по сравнению со значением изгибающего момента.
Чем больше у конструкции будет промежуточных опор, тем ближе ось листа будет к окружности. Однако при наличии промежуточных опор, ось листа между промежуточными опорами будет изгибаться по более сложной параболе при действии нагрузки. И чем меньше будет расстояние между промежуточными опорами, тем больше будет радиус окружности r, описывающей ось листа в местах максимальных напряжений, рисунки 2.б и 2.в. Таким образом минимально допустимый радиус изгибания листа ограничивается с одной стороны пластическими свойствами материала, а с другой стороны прикладываемой нагрузкой.
Точное определение минимально допустимого радиуса изгибания в связи с этим является достаточно сложной задачей, к тому же на расчеты непосредственно влияет прочность закрепления на опорах. Но как правило в точном расчете нет большой необходимости - если принимать минимальный радиус в 3-3,5 раза больше минимально допустимого упруго пластичными свойствами материала, то этого как правило достаточно для обеспечения работы материала в области упругих деформаций.
Вот только как определить это самый минимально допустимый радиус изгибания? Как ни странно но главным помощником в этом вопросе будет обычная начертательная геометрия и немножко алгебры. Приблизительно определить минимальный радиус изгибания можно, наложив окружность на эпюру прогибов. Например, для рассчитывавшегося в первом примере монолитного листа поликарбоната прогиб при двух опорах составил 51 см при пролете между опорами 42,5 см. При этом прогиб описывается формулой:
f = q(2lx3 -x4 - l3x) / 24EI
Оказывается эпюра прогибов - очень полезная штука, если построить ее с соблюдением размерности по оси х и по оси у, то окружность, которая будет иметь максимальное количество общих точек с параболой оси и даст ответ о минимально допустимом радиусе изгиба:
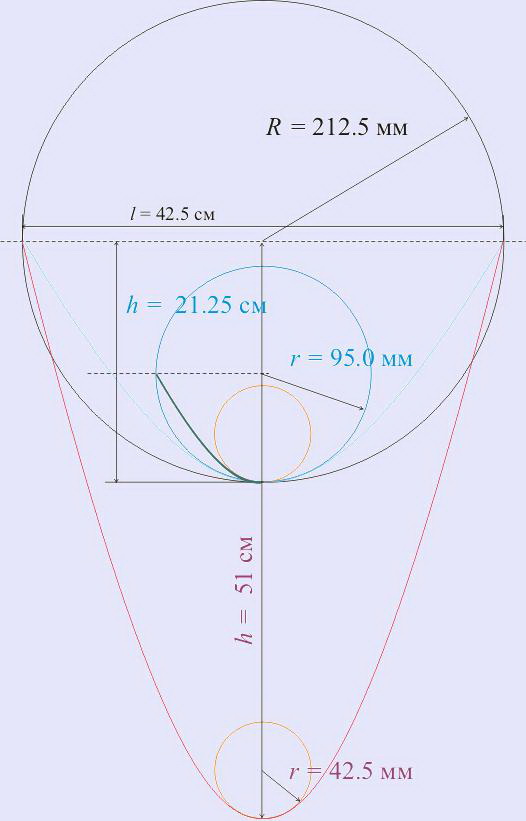
рис.3
Для рассчитывавшегося в первом примере монолитного листа поликарбоната была построена эпюра прогибов - красная линия на рис.3 Как видно из рисунка в месте максимальных внутренних напряжений эпюра прогибов описывается окружностью радиусом r = 42,5 мм (в 10 раз меньше длины пролета - красивая зависимость). Однако достигнуть такого радиуса изгибания для арочной конструкции, как я уже говорил, практически невозможно. Кроме того, чем длиннее будет участок листа, работающий в зоне предельно допустимых деформаций, тем больше вероятность, что упругие деформации перейдут в неупругие, проще говоря конструкция как минимум потеряет свою форму, как максимум - разрушится. Поэтому для монолитного листа поликарбоната толщиной 2 мм за минимально допустимый радиус изгибания можно принять 95 мм и даже 100 мм (для упрощения дальнейших расчетов). Тогда даже если у листа будет всего 2 опоры, то все равно ось листа в месте максимальных напряжений (показана на рис.3 темно зеленой линией) будет описываться окружностью минимально допустимого радиуса изгибания 42,5 мм, а при добавлении промежуточных опор, создающих радиус окружности около 95 мм, даже при очень больших нагрузках радиус окружности будет оставаться больше минимально допустимого и скорее произойдет разрушение из-за недостаточной прочности материала.
Однако при этом нельзя забывать, что рассматриваемый нами лист является не стержнем, а пластиной, для которой деформации по ширине листа также следует учитывать. Не то, чтобы эти деформации будут значительными, но скажем так, визуально заметными, т.е. эстетический вид листа ухудшится. Потому для снижения влияния, условно говоря, поперечных деформаций минимальный радиус изгибания желательно еще увеличить. Это следует сделать еще и потому, что нагрузка действующая на лист, далеко не всегда является равномерно распределенной, капли дождя, град, а тем более камни и прочие предметы, падающие на лист, следует рассматривать как сосредоточенную нагрузку. Так как предусмотреть все возможные виды нагрузок и их сочетание практически невозможно, то лучше для надежности увеличить минимально допустимый радиус еще в 2 раза.
Все это звучит несколько абстрактно и запутанно, потому, думаю, более понятной будет следующая формулировка:
Арочный настил из поликарбоната рассчитывается также как и плоский настил, при этом минимально допустимый радиус выгибания для поликарбонатного листа толщиной 2 мм составит 200 мм, для листа толщиной 3 мм - 300 мм, для листа толщиной 4 мм - 400 мм, для листа толщиной 6 мм - 600 мм, для листа толщиной 8 мм - 800 мм и так далее.
Примечание: увеличение высоты сечения в 2 раза приводит к увеличению момента сопротивления поперечного сечения в 4 раза. При этом максимально возможный расчетный пролет увеличивается в 2 раза, при этом соотношение величины прогиба к длине пролета остается неизменным, т.е. увеличение пролета в 2 раза приводит к увеличению прогиба в 2 раза, соответственно увеличение высоты поперечного сечения в 2 раза приводит к увеличению минимально допустимого радиуса в 2 раза. Тут может возникнуть и другой вопрос, ведь расчет производился на вполне определенную нагрузку, а между тем нагрузка может быть разная. Дело в том, что значение нагрузки не влияет на запас прочности и на минимально допустимый радиус. Например, уменьшение нагрузки в 4 раза приводит к увеличению минимально допустимого пролета в 2 раза. При этом прогиб увеличится также в 4 раза. Т.е. увеличение минимально допустимого пролета в 2 раза приведет к увеличению прогиба в 4 раза, значит радиус окружности, описывающей ось листа в месте максимальных напряжений, не изменится. Графически отображать это не стал.
Однако в большинстве рекомендаций по монтажу сотовых поликарбонатных листов даются другие значения минимально допустимого радиуса: для листа толщиной 4 мм минимально допустимый радиус изгибания - 700 мм, толщиной 8 мм - 1400 мм, толщиной 16 мм - 2800 мм. Правда при этом наличие перпендикулярных опор или вообще не рассматривается или просто не оговаривается их влияние на несущую способность. Подразумевается, что будут только параллельные опоры. Возможно, причина таких рекомендуемых значений еще и в том, что на лицевую (верхнюю) поверхность поликарбоната как правило наносится покрытие, защищающее поликарбонат от ультрафиолетового излучения. Насколько пластичным является такое покрытие, не известно, никаких данных по этому вопросу обнаружить не удалось. Тем не менее предполагаем, что производители перестраховываются.
Вот в общем-то и все, что хотелось сказать по поводу расчета настилов с использованием поликарбоната.
по материалам сайта "Доктор Лом"
|

