Расчет двухпролетных балок

   Когда Вы подшиваете лист гипсокартона к профилям, установленным с шагом 60 см, или когда укладываете короткую половую доску на три лаги, или заливаете бетоном плиту перекрытия, которая будет опираться на три стены (одну внутреннюю и две наружные), вы тем самым создаете двухпролетную балку. Для гипсокартона или половой доски принципиального значения это не имеет, а вот для монолитной железобетонной плиты имеет значение, и довольно большое, потому что арматуру монолитной двухпролетной плиты нужно рассчитывать и закладывать с учетом опорного момента на средней стене. Разница между двумя шарнирными балками с общей средней шарнирной опорой и неразрезной двухпролетной балкой с шарнирными опорами хорошо видна на следующем примере:

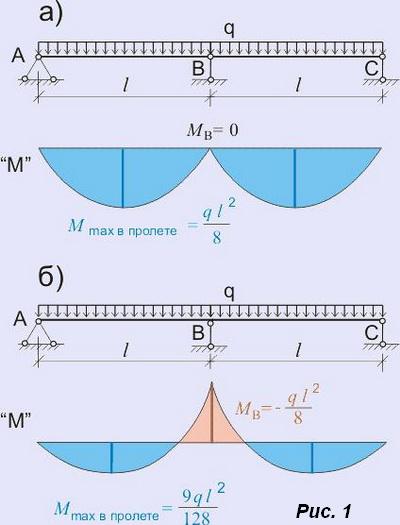
   Причем разница эта видна не по расчетным схемам, к которым нужно хорошо присмотреться, чтобы эту разницу увидеть, а по эпюрам изгибающих моментов. Как видно по эпюрам "М", в обычных однопролетных шарнирных балках со смежной опорой В только нижняя часть поперечного сечения балок растягивается, а верхняя - сжимается. В шарнирной двухпролетной балке растягивающие напряжения возникают в нижней части балки в области крайних опор и в верхней части балки на средней опоре. Казалось бы, ничего сложного, все достаточно просто и наглядно, нужно просто определить значение изгибающего момента на средней опоре В, но тут нас как раз и ожидает засада. Оказывается двухпролетные балки на шарнирных опорах являются один раз статически неопределимыми и значит обычных уравнений равновесия для определения момента на опоре не достаточно.

   Что такое статическая неопределимость? Женщины, те что попродвинутее, скажут, что это научное определение для давно известного выражения: "все мужики - козлы". Мужчины, изучающие сопромат в паузах между окучиванием вышеупомянутых женщин, скажут, что это ужас, летящий на крыльях ночи, кошмар неоперившегося птенца, выпавшего перед сессией с последнего этажа недостроенного небоскреба. А преподаватели завалят вас формулами и интегралами, иллюстрирующими кинематический, статический и энергетический методы расчета. И все по-своему будут правы. Ни в коей мере не оспаривая эти точки зрения, просто попробуем изложить один из методов расчета двухпролетной балки с максимальной долей наглядности.

   Итак. Давайте разбираться, что это за момент такой на средней опоре, откуда он взялся и как влияет на расчетные параметры балки.

   Если рассматривать двухпролетную балку на шарнирных опорах А, В и С как однопролетную на опорах А и С, то чтобы соблюсти принцип равновесия сил, мы должны в точке В приложить некоторую силу, другими словами сосредоточенную нагрузку, которая и будет опорной реакцией балки. Эта опорная реакция будет направлена вверх, что логично, если основная равномерно распределенная нагрузка направлена вниз. Если мы строим эпюру моментов для однопролетной шарнирной балки при действии сосредоточенной нагрузки, то получаем следующий результат:

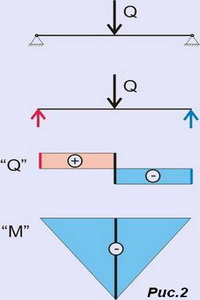
   Если мы проведем пунктирные линии от максимального значения момента на промежуточной опоре В (рис.1.б) к крайним опорам А и С, то мы получим эпюру моментов от действия опорной реакции В (на рис. 2 обозначена бежевым цветом):

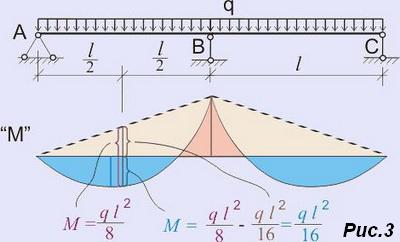
   По сути эта эпюра, представляющая собой треугольник, ничем не отличается от показанной на рис.2, вот только сила - опорная реакция - у нас направлена в противоположную сторону, потому и эпюра расположена сверху. А еще получается, что итоговая эпюра изгибающих моментов представляет собой сумму эпюр от распределенной нагрузки (рис. 1.а) и от опорной реакции В. И если это так, то значение изгибающего момента посредине пролета равно разнице этих эпюр. Осталось только выяснить, чему же именно равен момент на промежуточной опоре В.

Примечание: Понятия "положительный момент" и "отрицательный момент" очень условные. Можно считать, что момент в пролете отрицательный, как показано на рис. 2 и тогда момент на опоре - положительный. Это выглядит достаточно разумно, когда эпюра расположена снизу оси х. Но в технической литературе чаще встречаются противоположные обозначения: когда эпюра расположена ниже оси х - момент положительный, а когда выше оси х - отрицательный. Чтобы в дальнейшем не путаться, будем обозначать моменты так, как принято в технической литературе.

   Как мы уже говорили, определить значение момента и значения опорных реакций для двухпролетной балки, используя только обычные уравнения равновесия, не представляется возможным, но на этот случай у нас есть козырь в рукаве. Мы должны помнить, что под действием нагрузки балка прогибается (точнее центр тяжести поперечного сечения балки, расположенного на некотором расстояния от начала балки по оси х, смещается по оси у относительно оси х на некоторую величину f), при этом поперечные сечения балки далеко не всегда перпендикулярны оси х, а имеют некоторый наклон, выражаемый углом θ. А это значит, что какие бы нагрузки не действовали на рассматриваемую балку, прогиб f на опорах такой балки будет равен 0 (так как балка у нас на не подвижных опорах), а в данном случае и угол поворота поперечного сечения балки на опоре В также равен нулю. Эти знания позволяют составить нам столько дополнительных уравнений, сколько нужно. Например:

   Так как балка у нас симметричная и нагрузка на балку равномерно распределенная по всей длине, то нам достаточно рассматривать не всю балку а только левую или правую часть, как отдельную балку. Опорные реакции для такой балки будут равны

при этом данное уравнение будет справедливо и для правой части балки:

а суммарная опорная реакция на опоре В для двухпролетной балки будет составлять:

   Чтобы такое допущение было корректным, мы должны приложить на опоре В для левой балки такой момент М, при действии которого угол поворота поперечного сечения балки на опоре В будет равен нулю, при этом на правую балку на опоре В будет действовать такой же момент М, но направленный в противоположную сторону. В этом случае суммарный момент для двухпролетной балки на опоре В будет равен нулю, и скачка на общей эпюре моментов не будет, так как моменты приложены в одной точке равны по значению и противоположны по знаку.

   При действии изгибающего момента М как ни крути, а возникают опорные реакции. При этом опорная реакция на опоре А:

а опорная реакция на опоре В:

   Таким образом общая опорная реакция на опоре А будет составлять:

а общая опорная реакция на опоре В будет составлять:

   Угол поворота θ поперечного сечения балки на опоре А и на опоре В для однопролетной балки при данной нагрузке составляет:

   При действии изгибающего момента на опоре В угол поворота θ поперечного сечения балки на опоре А для однопролетной балки составляет:

а на опоре В:

   Таким образом суммарный угол поворота на опоре А составит:

а на опоре В:

это уравнение (1.6.2) в данном случае и является тем самым дополнительным уравнением, позволяющим определить все накопившиеся неизвестные.

   Из уравнения (1.6.2) мы путем простейших математических преобразований получаем значение момента на опоре В:

   Зная значение момента на опоре В, мы можем определить реакции опор по формулам (1.3) и (1.1):

   Зная опорные реакции и углы поворота на опорах, мы можем определить все необходимые параметры для нашей балки, хоть деревянной, хоть металлической, хоть железобетонной, но сначала не помешает решить, например уравнение угла поворота:

так как угол поворота поперечного сечения на опоре В равен нулю, то:

   Все это хорошо, скажете Вы но как определить момент на опоре, если нагрузка к балке приложена не симметрично и значит угол поворота на опоре В не равен 0? Для ответа на этот вопрос мы рассмотрим

   Если нагрузка действует только на один пролет двухпролетной балки, при этом длины пролетов равны, то значение момента на опоре В уменьшится в 2 раза

по той простой причине, что теперь момент действует не на один пролет, как в первом примере, а на два пролета. Таким образом значение искомого момента на опоре В будет:

Тогда по формулам (1.3) и (1.1):

а так как на правую часть балки нагрузка не действует, а действует только изгибающий момент, то

   И еще, из этого следует, что двухпролетную балку с равными пролетами и симметрично распределенной нагрузкой, рассмотренную в первом примере, можно рассматривать как две отдельные двухпролетные балки с равными пролетами, при этом у первой балки загружен первый пролет, а у второй балки - второй пролет. В принципе это настолько просто, что подробно и запутанно объяснить это очень сложно.

   Хорошо, допустим, скажете Вы, но как быть, если пролеты у балки не равны? Для ответа на этот вопрос мы рассмотрим

   В данном случае двухпролетную балку проще рассматривать как две отдельные двухпролетные балки. Если равномерно распределенная нагрузка приложена только к первому пролету балки, то значение момента на опоре В будет:

   Если равномерно распределенная нагрузка приложена только ко второму пролету балки, то значение момента на опоре В будет:

Если равномерно распределенная нагрузка приложена к обоим пролетам балки, то значение момента на опоре В будет:

   Из этих уравнений мы можем сделать еще несколько интересных выводов - если пролеты равны, то мы получаем уравнение (2.1) при нагрузке, действующей на один пролет, или уравнение (1.6.4) при нагрузке, действующей на оба пролета, а если длина второго пролета равна 0, то мы получаем уравнение (1.6.4) и одновременно однопролетную балку с шарнирной опорой А и жестким защемлением на опоре В. Поэтому двухпролетную балку из первого примера с равными пролетами и равномерно распределенной нагрузкой можно рассматривать как две однопролетные балки у которых одна опора шарнирная, а вторая - жесткое защемление. Такие однопролетные балки также являются один раз статически неопределимыми, но как бороться с этой статической неопределимостью, мы теперь знаем.

   С определением опорных реакций для двухпролетной балки с разными пролетами больших проблем в принципе нет, однако формулы из-за различных значений пролетов получаются достаточно громоздкими.

При действии равномерно распределенной нагрузки только в первом пролете l₁:

При действии равномерно распределенной нагрузки только во втором пролете l₂:

Суммарные опорные реакции:

   Не смотря на столь страшный вид, при решении конкретных задач, когда известны значения пролетов, то все выглядит не так уж страшно. Например, нужно рассчитать шарнирно опертую балку с пролетами l₁ = 2,6 м и l₂ = 1,4 м на действие равномерно распределенной по всей длине балки нагрузки q.

   Определим сначала значения общих выражений

8(l₁ + l₂) = 8(2,6 +1,4) = 32
и
l₁³ + l₂³ = 2,6³ + 1,4³ = 17,576 + 2,744 = 20,32

разделим 20,32/32 = 0,635, чтобы получить общий член для большинства уравнений

А = ql₁/2 - q(l₁³ + l₂³)/(8l₁(l₁ + l₂)) = 2,6q/2 - 0,635q/2,6 = 1,0558q

B = q(l₁ + l₂)/2 + q(l₁³ + l₂³)/(8l₁(l₁ + l₂)) + q(l₁³ + l₂³)/(8l₂(l₁ + l₂)) = 4q/2 + 0,635q/2,6 + 0,635q/1,4 = 2,6978q

С = ql₂/2 - q(l₁³ + l₂³)/(8l₂(l₁ + l₂)) = 1,4q/2 - 0,635q/1.4 = 0,2464q

Сумма опорных реакций должна быть равна суммарной распределенной нагрузке на 4 метрах балки. Проверяем:

A + В + С = 1,0558q + 2,6978q + 0,2464q = 4q

   Позвольте, но ведь нагрузка бывает не только равномерно распределенной, скажете Вы, как быть в этом случае? А в этом случае достаточно ознакомиться с расчетными формулами для двухпролетных балок, выведенными по этому принципу, или найти уравнение трех моментов, которое подходит для любого случая загружения.