На пружину кручения действует пара сил, закручивающая ее в поперечных сечениях.
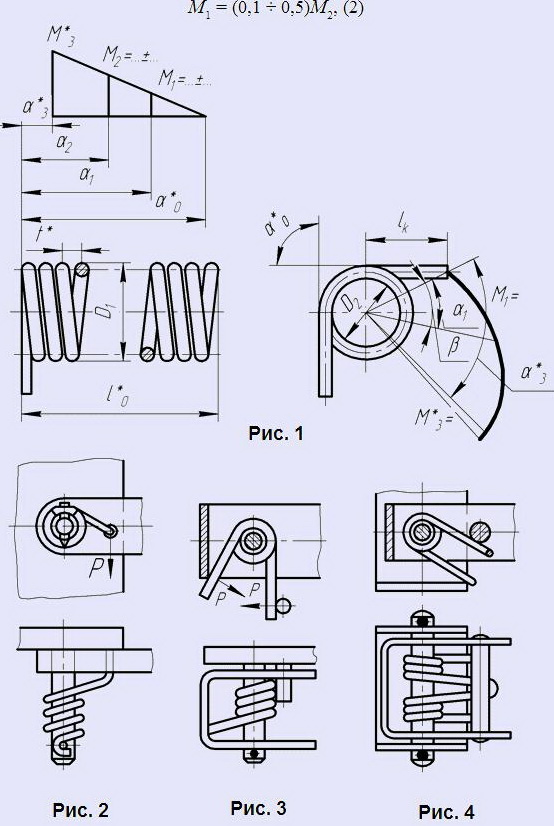
Пружины применяют в качестве прижимных аккумулирующих и упругих звеньев силовых передач. Примеры применения даны на рис. 2, 3, 4.
Расчет. Исходные данные:
- наибольший рабочий крутящий момент M2, Н·мм;
- наибольший yгол закручивания α2, град.
Находим наибольший рабочий крутящий момент в Н·мм
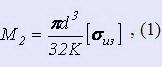
Наименьший (установочный) рабочий крутящий момент определяется условиями работы механизма, его значение в Н·мм
Если установочная нагрузка не предусматривается, то М1 = 0.
Предельно допустимый крутящий момент (для наибольшей испытательной нагрузки) в Н·мм:
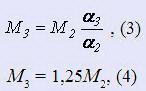
Индекс пружины
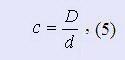
здесь D - средний диаметр пружины; рекомендуется принимать с >= 5 (чем меньше d, тем больше следует брать с); в исключительных случаях допустимо с = 4.
Значения индекса пружины с можно принимать в зависимости от диаметра проволоки:

Коэффициент формы сечения и кривизны витка
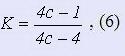
Диаметр проволоки в мм

Напряжение нормальное при изгибе в МПа под нагрузкой М2
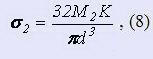
должно быть σ2 ≤ [σиз]
Предельный угол закручивания в градусах при M3
α3 = 1,25·α2, (14)
Наибольший рабочий угол закручивания в градусах при М1
α2 ≈ 8α3, (34)
Наименьший рабочий угол закручивания в градусах при М1
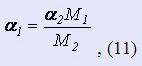
Рабочий угол закручивания в градусах от М1 до М2
Θ = α2 - α1, (12)
Обычно определяют из условий работы механизма.
Число рабочих витков
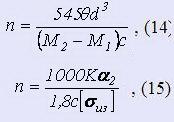
Наименьшее число витков (из условия устойчивости пружины, т. е. постоянства ее оси)
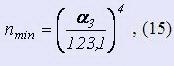
должно быть n >= nmin
Высота пружины в свободном состоянии в мм
lo = (n + 1)d + nδ, (16)
Зазор между витками в мм
δ = 0,1...0,5, (17)
Шаг пружины в мм
t = d + δ, (18)
Длина развернутой пружины в мм
lo ≈ 3,2Don + lприц, (19)
lприц - длина проволоки прицепов, мм.
Пример расчета. Дано: наибольший рабочий крутящий момент М2 = 11000 Н·мм, наибольший рабочий угол закручивания α2 = 140°; пружина класса 1, разряда 3.
Решение. Допускаемое напряжение на изгиб в МПа
[σиз] = 1,25[τ3]
Из табл. 2 ("Классы и разряды пружин") выбираем для стали 60С2А [τ3] = 560 МПа
[σиз] = 1,25·560 = 700 МПа
Индекс пружины по формуле 5 принимаем с = 8.
Коэффициент формы сечения и кривизны витков по формуле 6
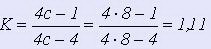
Диаметр проволоки по формуле 7

принимаем d = 6 мм.
Обозначение: Проволока 60С2А-1-П-6,0 ГОСТ 14963-78
Диаметр пружины по формуле 5
D = cd = 8 · 6 = 48 мм;
D1 = D + d = 48 + 6 = 54 мм;
D2 = D - d = 48 - 6 = 42 мм.
Иногда диаметр пружины приходится принимать по конструктивным соображениям.
Нормальное напряжение при М2 (т. е. поверочный расчет пружины на прочность) по формуле 8
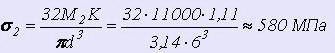
Число рабочих витков по формуле 14
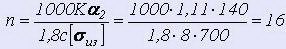
Предельный угол закручивания по формуле 14
α3 = 1,25α2 = 1,25 · 140 = 175°
Наименьшее число витков по формуле 15
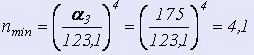
Наименьший рабочий крутящий момент по формуле 2
М1 = 0,2M2 = 0,2 · 11000 = 2200 Н·мм
Наименьший рабочий угол закручивания по формуле 11
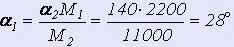
Зазор между витками по формуле 17
δ = 0,5 мм.
Высота пружины по формуле 16
lo = (n + 1)d + nδ = (16 + 1)·6 + 16 · 0,5 = 110 мм
Предельно допустимый крутящий момент по формуле 4
М3 = 1,25M2 = 1,25 · 11000 = 13750 Н·мм
Шаг пружины по формуле 18
t = 6 + 0,5 = 6,5 мм
Длина развернутой проволоки - по формуле 19.
Примечание. Если конструкция пружины окажется не совсем удачной, расчет следует повторить, исходя из иного, вновь выбранного индекса пружины.
Пример выполнения элементов чертежа пружины кручения
с прямыми концами, расположенными вдоль оси пружины

Похожие документы:
расчет пружин сжатия и растяжения;
расчет пластинчатой пружины изгиба;
чертеж пружины сжатия;
чертеж пружины параболоидной;
ГОСТ 13764-86 - "Пружины винтовые цилиндрические сжатия и растяжения из стали круглого сечения. Классификация";
ГОСТ 13766-86 - "Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 1 из стали круглого сечения. Основные параметры витков";
ГОСТ 13767-86 - "Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 2 из стали круглого сечения. Основные параметры витков";
ГОСТ 13768-86 - "Пружины винтовые цилиндрические сжатия и растяжения 1 класса, разряда 3 из стали круглого сечения. Основные параметры витков";
ГОСТ 13769-86 - "Пружины винтовые цилиндрические сжатия 1 класса, разряда 4 из стали круглого сечения. Основные параметры витков";
ГОСТ 13770-86 - "Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 1 из стали круглого сечения. Основные параметры витков";
ГОСТ 13771-86 - "Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 2 из стали круглого сечения. Основные параметры витков";
ГОСТ 13772-86 "Пружины винтовые цилиндрические сжатия и растяжения II класса, разряда 3 из стали круглого сечения. Основные параметры витков";
ГОСТ 13773-86 - "Пружины винтовые цилиндрические сжатия II класса, разряда 4 из стали круглого сечения. Основные параметры витков";
ГОСТ 13774-86 - "Пружины винтовые цилиндрические сжатия III класса, разряда 1 из стали круглого сечения. Основные параметры витков";
ГОСТ 13775-86 - "Пружины винтовые цилиндрические сжатия III класса, разряда 2 из стали круглого сечения. Основные параметры витков";
ГОСТ 13776-86 - "Пружины винтовые цилиндрические сжатия III класса, разряда 3 из стали круглого сечения. Основные параметры витков".
| 
