
В статье показана возможность и целесообразность использования червячных передач, содержащих цилиндрический червяк и эвольвентное косозубое колесо, для механизмов, в которых одно из звеньев передачи должно совершать винтовое движение.
Сформулированы условия сопряженности зацепления в рассматриваемых передачах. Показан алгоритм геометрического и технологического расчета, обеспечивающий возможность изготовления червяков с учетом возможностей токарно-винторезных и червячно-шлифовальных станков и нарезания зубьев колеса стандартными червячными фрезами. Осевой модуль червяка выбирается с учетом возможностей станков, а равенство основных модулей червяка и колеса осуществляется за счет коррекции осевого угла профиля.

Червячные механизмы, в которых без нарушения сопряженности зацепления одно из звеньев (червяк или колесо) может совершать винтовое движение вокруг и вдоль своей оси с ходом, отличным от хода его собственной винтовой поверхности, могут весьма эффективно использоваться в современной технике. При этом звено, совершающее винтовое движение, может быть выполнено за одно целое с рабочим звеном, что в сочетании с высокой редукционной способностью передачи позволяет свести к минимуму число звеньев кинематической цепи такого устройства. Тем самым уменьшается сумма боковых зазоров, величина рассогласования между положениями входного и выходного звеньев и, в конечном счете, повышается точность механизма.
Давайте рассмотрим два примера использования червячных передач с винтовым движением звеньев в механизмах прокатного оборудования.
ПЕРЕДАЧА С ВИНТОВЫМ ДВИЖЕНИЕМ КОЛЕСА
В МЕХАНИЗМЕ ОСЕВОЙ РЕГУЛИРОВКИ ВАЛКА ШАРОПРОКАТНОГО СТАНА
Высокопроизводительным методом производства шаров является горячая винтовая прокатка между двумя калибровочными валками, которые скрещиваются под небольшим углом. Точность получаемых шаров определяется, прежде всего, точностью взаимного положения рабочих валков.
Осевая регулировка положения валка осуществляется с помощью показанного на рис.1 устройства для преобразования вращения вала двигателя в винтовое движение рабочего звена. Рабочий валок 1 размещен в стакане 4, на наружной поверхности которого нарезаны упорная резьба 2 с шагом Т и эвольвентный косозубый венец 3.
Венец 3 выполнен с числом зубьев z2, нормальным модулем mn и делительным углом наклона зуба β2. Осевой ход Pz винтовой поверхности его зубьев определяется выражением:
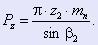 (1) (1)
Стакан приводится в винтовое движение относительно гайки 6, неподвижно закрепленной в корпусе клети 7, посредством червяка 5 с числом заходов z1 .
За один оборот червяка рабочее звено (рабочий валок со стаканом) поворачивается на угол ψ и одновременно перемещается вдоль своей оси на величину L1, связанную с шагом Т, условием:
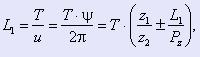 (2) (2)
где, u – передаточное число механизма.
Решая уравнение (2), получим выражение для линейного перемещения L рабочего звена за n1 оборотов червяка:
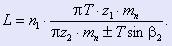 (3) (3)
Знак “+” ставится в случае, если зубья венца 3 и резьба гайки 2 имеют противоположное направление винтовой линии, а “– “в случае, если их направления совпадают.
Расчет геометрических параметров передачи выполняется из условия сопряженности зацепления по предложенному ниже алгоритму. Отметим только, что для передач этого вида червяк обычно выполняется однозаходным, а угол β2 наклона зубьев венца не превышает 8o. При этом осевой модуль mx1 червяка может быть выбран из стандартного ряда равным нормальному модулю mn фрезы, нарезающей зубья венца.
МЕХАНИЗМ С ВИНТОВЫМ ДВИЖЕНИЕМ ЧЕРВЯКА
В УСТРОЙСТВЕ ИНДИКАЦИИ РАДИАЛЬНОГО ПЕРЕМЕЩЕНИЯ ВАЛКА
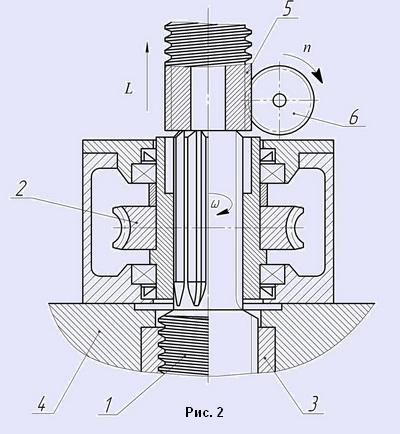
Устройство индикации, представленное на рис.2, предназначено для настройки рабочих валков станов винтовой или продольной прокатки на радиальный размер. Это устройство включает в себя нажимной винт 1, который скользит по шлицам внутри ступицы червячного колеса 2 и поддерживается резьбой гайки 3, фиксированной в корпусе 4, совершая, таким образом, винтовое движение с шагом T, равным шагу гайки. Свободный конец нажимного винта несет на себе червяк 5 с шагом t и числом заходов z1, который приводит в движение косозубое эвольвентное колесо 6, установленное на входном валу датчика угла поворота.
Исходными данными для расчета устройств такого типа являются число импульсов датчика угла поворота N и цена одного импульса μ. По этим параметрам линейное перемещение нажимного винта за полный оборот вала датчика L = N μ.
Исходя из требуемого линейного перемещения L, передаточное число передачи u, то есть отношение числа оборотов n1 винта и жестко связанного с ним червяка к числу оборотов n2 колеса, насаженного на вал датчика, находим как:
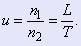 (4) (4)
Для того чтобы в таком устройстве перемещение рабочего валка на целое число миллиметров соответствовало целому числу импульсов, червяк должен быть выполнен с метрической резьбой. Число зубьев колеса определяется в зависимости от шага червяка t, направления и числа его заходов z1 выражением:
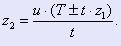 (5) (5)
При этом t и z1 должны быть выбраны таким образом, чтобы число z2 получалось целым и при этом лежало в разумных пределах ( z2 = 20…50). Из выражений (4) и (5), выполнив необходимые преобразования, получим формулу для линейного перемещения рабочего звена за один оборот вала датчика в виде:
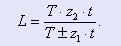 (6) (6)
Кроме того, шаг червяка должен быть выбран таким образом, чтобы для его осевого модуля mx1 = t / π, можно было найти из стандартного ряда меньшее, но достаточно близкое значение нормального модуля mn0 фрезы, используемой для нарезания зубьев колеса. При этом колесо может выполняться и с глобоидной формой зубчатого венца, однако учитывая, что диаметр червяка в таком механизме существенно больше диаметра колеса, венец целесообразно выполнять цилиндрическим. Далее расчет передачи выполняется по предложенному ниже алгоритму.
Подчеркнем, что оба рассматриваемых механизма являются одноподвижными, и передаточное число в них определяется вполне однозначно. При этом оно зависит не только от отношения числа зубьев z2 колеса к числу заходов z1 червяка, но и от отношений шага T гайки к осевому ходу Pz зубчатого венца в первом случае и осевому ходу t·z1 червяка во втором случае.
УСЛОВИЯ СОПРЯЖЕННОСТИ ЗАЦЕПЛЕНИЯ
В свое время ортогональные передачи зацеплением, состоящие из цилиндрического червяка и цилиндрического косозубого колеса, были хорошо известны и рассматривались в ряде учебников и справочников по теории механизмов и машин, в частности в книгах, А.П. Малышева «Кинематика механизмов», «Червячная передача», Д.С. Зернова и др. «Прикладная механика», В.В. Добровольского «Теория механизмов».
Такие передачи можно проектировать как корригированные винтовые передачи с малым числом зубьев шестерни, используя известные методы расчета, изложенные в работах Курлова Б.А. «Винтовые эвольвентные передачи». В этом случае активные поверхности витков червяка и зубьев колеса получаются эвольвентными винтовыми с равным нормальным модулем. Этот способ неудобен тем, что осевой модуль червяка получает некоторое дробное значение, которое трудно обеспечить при нарезании червяка на токарно-винторезных и червячно-шлифовальных станках.
Второй известный метод синтеза таких передач состоит в том, что червяк проектируется, как эвольвентный, со стандартным осевым модулем, которому должен быть равен торцовый модуль колеса. При этом нормальный модуль колеса получится нестандартным и потребует для нарезания зубьев изготовления специальной фрезы, что тем более неудобно для практики.
Технологически более удобный метод синтеза, предложенный в данной статье, основан на известной теореме Л.В. Коростелева из книги «Образование зубчатых передач с переменным расположением осей колес». Согласно этой теореме, если активные поверхности зубьев колес образованы инструментом с эвольвентными производящими поверхностями одно- или двухпараметрическим огибанием при постоянном отношении угловых скоростей заготовки и инструмента, то эти поверхности будут гарантировано сопряженными, то есть в такой передаче будет сохраняться постоянное передаточное отношение при любых погрешностях в расположении осей колес.
Из этой теоремы, в частности следует, что для сопряженности червячной передачи необходимо и достаточно, чтобы у червяка и червячной фрезы, нарезающей зубья колеса, были равны между собой основные шаги, то есть расстояния между соседними витками, измеренные по нормали к активной поверхности.
Поскольку фреза автоматически переносит на колесо свой основной шаг, то, переходя от шагов к модулям, условие сопряженности активных поверхностей звеньев рассматриваемой передачи можно записать в виде:
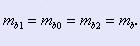 (7) (7)
Здесь mb1 и mb0 – основные модули, соответственно червяка и фрезы, связанные с нормальными модулями mn1 и mn0 и нормальными углами профиля αn1 и αn0 известными зависимостями:
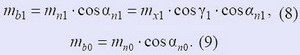
где,
γ1 = arctan (mx1 z1 / d1) – делительный угол подъема витка червяка,
mx1 – осевой модуль,
z1 – число заходов,
d1 – делительный диаметр.
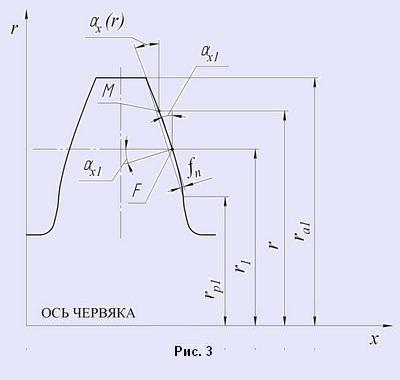
В процессе реального проектирования конструктор, прежде всего, должен выбрать червячную фрезу из числа стандартных со стандартными значениями угла профиля αn0 = 20o и нормального модуля mn0. Осевой модуль mx1 червяка выбирается с учетом возможностей червячно-шлифовального станка. Равенство основных модулей червяка mb1 и колеса mb2, осуществляется за счет коррекции осевого угла профиля αx1 (рис.3). Соблюдение заданного межосевого расстояния достигается высотной коррекцией зубьев колеса.
 АЛГОРИТМ РАСЧЕТА
АЛГОРИТМ РАСЧЕТА
Предлагаемая методика расчета применима к обоим рассмотренным выше типам передач. Она построена на том дополнительном условии, что расчетную точку контакта мы размещаем в средней плоскости колеса на его начальном цилиндре, т.е. в полюсе P зацепления (рис.4 и рис.5). В этой точке мы должны обеспечить равенство между собой осевого угла αxw1 профиля витка и торцового угла αtw2 профиля зуба колеса, а также угла γw1 подъема витка и угла βw2 наклона зуба.
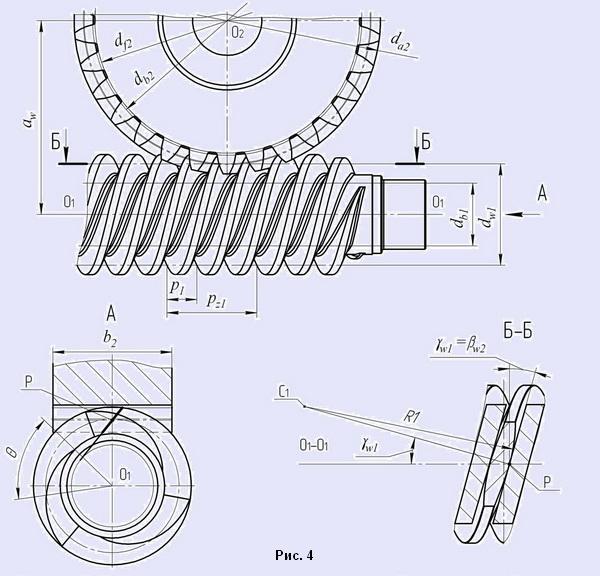
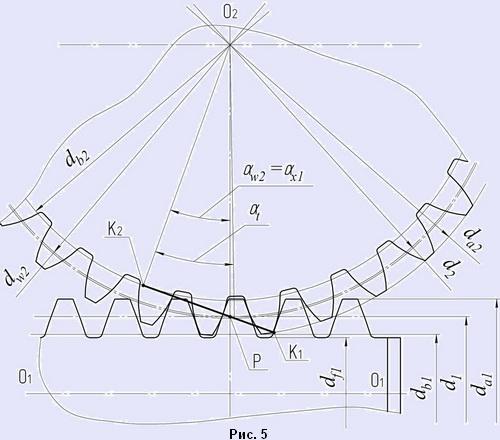
Исходными данными для расчета служат: осевой модуль червяка mx1, нормальный модуль фрезы mn0, число заходов червяка z1, межосевое расстояние передачи aw и делительный диаметр червяка d1 = qmx1.
Исходя из этих данных, прежде всего, определяем по выражению (8) основной модуль передачи mb. Затем рассчитываем параметры червяка на его основном цилиндре:
основной угол подъема: λ = arccos (mb / mx1),
модуль в торцовом сечении: mtb1 = mb / sin λ,
и диаметр основного цилиндра: db1 = z1 mtb1.
В системе координат, ось x которая направлена вдоль оси червяка, осевой профиль эвольвентного червяка описывается уравнением [9]:
x(r) = 0,5·mx1· z1(tan(θ(r)) - θ(r)), (10)
где,
r – текущий радиус червяка,
θ(r) = arccos(0,5db1 / r) - угол развернутости эвольвенты в торцовом сечении.
Осевые углы профиля витка червяка в текущей точке αx (r) и на делительном цилиндре αx1 определяем дифференцированием выражения (10):
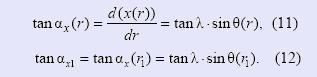
Углы подъема витка червяка в текущей точке на делительном и начальном цилиндрах определяются выражениями:
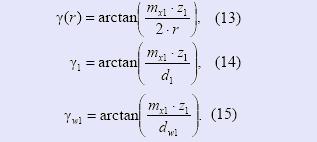
Повторным дифференцированием угла αx (r) получаем выражение для кривизны осевого профиля K(r) в произвольной точке:
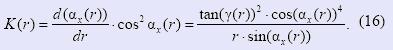
С достаточной для практических целей точностью эвольвентный червяк может шлифоваться как квазиархимедов, т.е. его осевой профиль должен быть выполнен с делительным углом αx1, рассчитанным по формуле (12), и на рабочей высоте витка h = 2 mn0 иметь небольшую стрелку выпуклости:
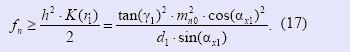
Число зубьев z2 сопряженного колеса находим как целую часть выражения:
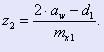 (18) (18)
Исходя из условия равенства угла γw1 подъема витка и угла βw2 наклона зуба, определяем делительный угол β2 наклона зуба колеса:
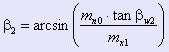 (19) (19)
По найденному значению β2 последовательно определяем: торцовый делительный угол профиля: торцовый делительный модуль:
mt=mn0 / cosβ2, (20)
торцовый делительный угол профиля:
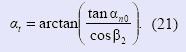
При проектировании передачи необходимо следить за тем, чтобы расчетная точка Р, лежащая на начальном цилиндре, была расположена вблизи делительного цилиндра червяка, т.е. коэффициент смещения x2 = (2аw – d1 – d2) / 2mx1 находился в пределах: – 0,1 < x < +0,25.
Определение контурных и зубоизмерительных параметров передачи, таких, как диаметры выступов dа1,2 и впадин dƒ1,2 червяка и колеса, делительный d2, основной db2 и начальный dw2 диаметры колеса, толщина зуба колеса Sw2, толщина витка червяка Sw1, длина общей нормали Wn и т.д. выполняется по стандартным формулам.
В таблицу сведены результаты расчета нескольких спроектированных и изготовленных червячных передач, содержащих квазиархимедов червяк и эвольвентное косозубое колесо. Расчет выполнялся по описанной выше методике, реализованной в среде MathCAD.
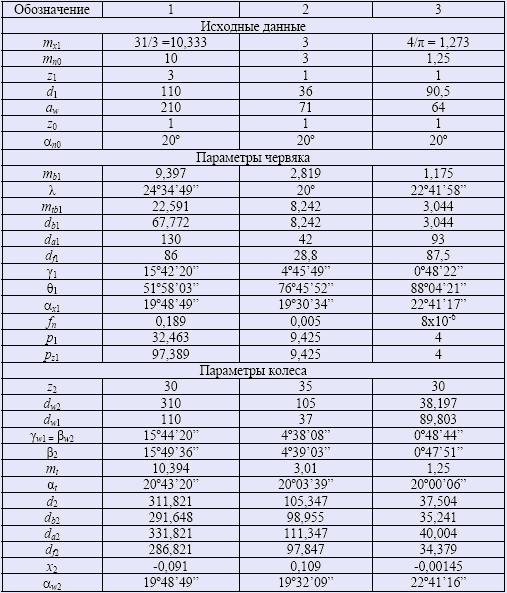
Такой расчет можно выполнить и в среде КОМПАС-3D в библиотеке "Валы и механические передачи":
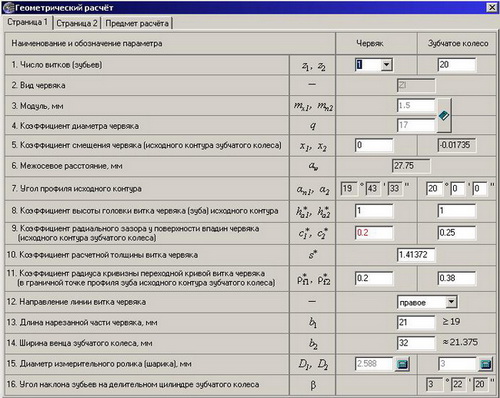
По результатам расчета мы получаем два чертежа: червяка и косозубой шестерни. Червяк изготавливается на токарно-винторезном станке с использованием прямого резца и стандартного модуля и шлифуется на червячно-шлифовальном станке. Косозубое колесо изготавливается с применением стандартной червячной фрезы.

Таким образом, мы рассмотрели возможность и целесообразность использования червячных передач, содержащих цилиндрический червяк и эвольвентное косозубое колесо, для механизмов, в которых одно из звеньев передачи должно совершать винтовое движение. Привели примеры их использования в приводах и системах управления, где они позволяют свести к минимуму число звеньев и сумму зазоров в кинематической цепи и тем самым повысить точность получаемых изделий. Привели алгоритм геометрического и технологического расчета, обеспечивающего возможность изготовления червяков с учетом возможностей токарно-винторезных и червячно-шлифовальных станков и нарезания зубьев колеса стандартными червячными фрезами.
в статье использован материал работы С.А. Лагутина и Е.А. Гудова
"Червячные механизмы с винтовым движением звеньев".
Похожие документы:
расчет ходовых винтов;
расчет грузовых винтов;
| 
